A galaxy of prime numbers

Most mathematicians know that the representation of prime numbers $p$ in polar coordinates $(r,\theta) = (p,p)$ results in a cool-looking spiral.

For now, this will not be an in-depth overview.

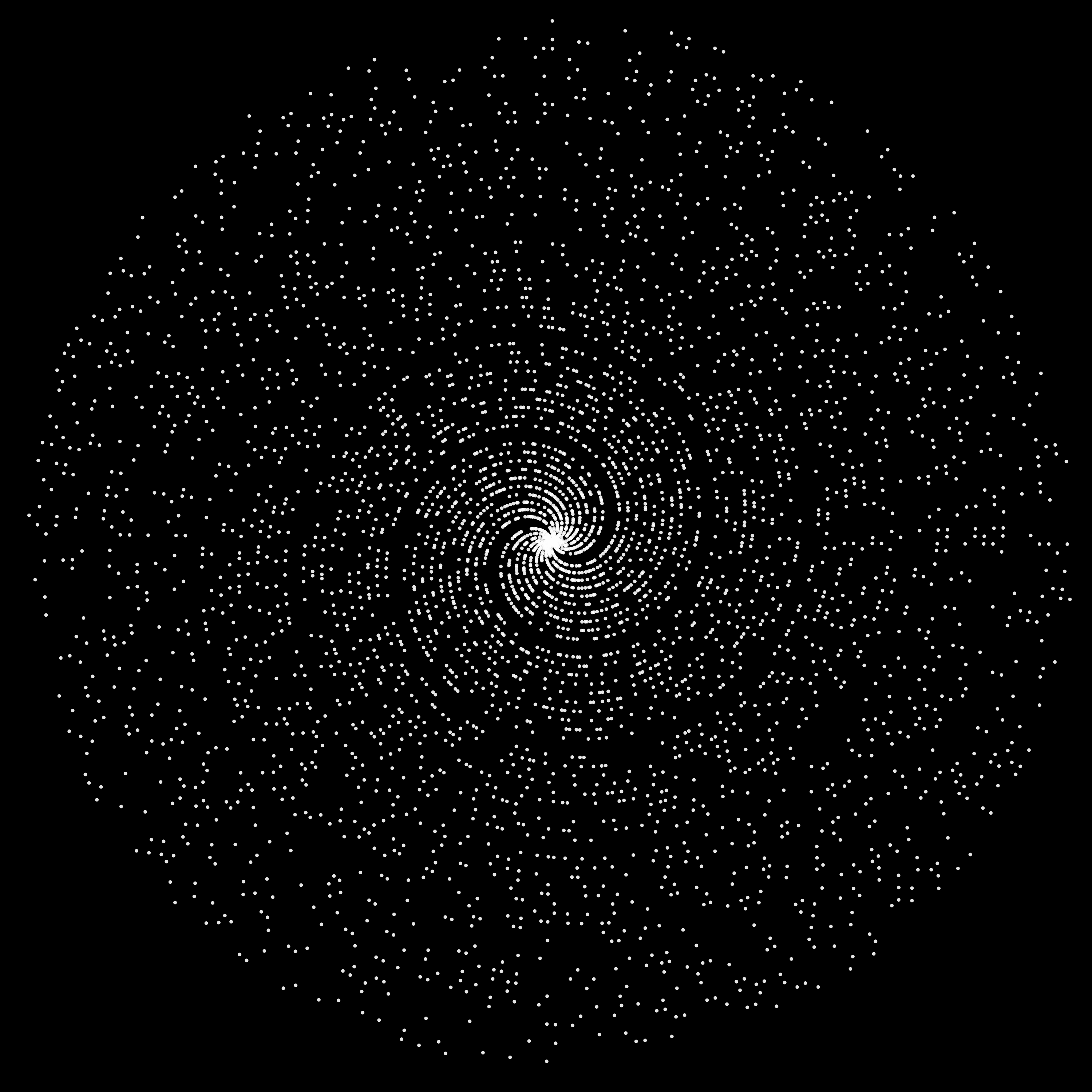
One day I noticed that it looks quite like a galaxy: a "barred spiral galaxy" to be precise, like our own! Can we add more to it?

Star classes

Astronomers classify stars according to their spectral characteristics. I enjoy astronomy, and I am (partially) confident they know what they are doing.

The following can be found on Wikipedia [1], and is a list of star classes in order of temperature:

Star class	Chromaticity	Percentage
O	blue	0.00003%
B	bluish white	0.12%
A	white	0.61%
F	yellowish white	3.00%
G	yellow	7.60%
K	light orange	12.00%
M	yellowish white	76.00%

A cool fact is that they can be memorised with the mnemonic "Our Bright Astronomers Frequently Generate Killer Mnemonics!" and to each class corresponds a different color ("chromaticity"). That is not how we see them from earth, filtered by the atmosphere, but rather how they look from space. In the words of Mitchell Charity [2],

The colors here are for the big balls of hot gas in space, rather than the pin-pricks of light in the local sky.

These pesky astronomers are clearly having fun and we are missing on it.

Prime number classes

My idea was to compare the frequency of star classes to the frequency of (some) prime number classes, and to each associate the respective chromaticity. This is a tricky business: to build an interesting plot we should use meaningful classes, but also keep them close to the star classes frequencies.

How many primes?

I noticed that adding too many prime numbers makes for a weird-looking spiral. Doing some tests, stopping at around $40000$ returned the closest thing to our galaxy. There are $4203$ primes up to $40000$, and we must keep it in mind to get matching percentages.

Which primes?

Now, we have to find the correct prime number classes. Remember that we are considering all primes up to $40000$: what is the frequency of each class? For the algebra nerds among us, this table represents all candidate classes and my conclusions. The wisest among you might wish to skip it.

Prime number class	Percentage	Well-known?
Balanced	4.95%	❌
Circular primes	0.79%	❌
Cousin primes	27.62%	❌
Cullen primes	0.000025%	❌
Emirps (reversible primes)	23.32%	❌
Even primes	0.000025%	✅
Fermat primes	0.12%	✅
Fibonacci primes	0.19%	✅
Happy primes	16.35%	❌
Mersenne primes	0.10%	✅
Palindromic primes	1.67%	❌
Pythagorean primes	49.41%	❌
Primorial primes	0.21%	❌
Safe primes	7.76%	✅
Sophie-Germain primes	13.44%	✅
Strobogrammatic primes	0.17%	❌
Strong primes	48.94%	✅
Twin primes	28.10%	✅

Let us have a look at the lucky winners.

Circular primes are stubborn numbers that keep being prime even if one rotates their digits. An example is $37\rightarrow73$, but also $113\rightarrow131\rightarrow311$.

Even primes are those primes that are also odd. Unsurprisingly, $2$ is the only one.

Mersenne primes are those of form $2^n-1$ for some integer $n$, they are very well-known for the (original) Mersenne conjecture.

Palindromic primes are primes where their palindrome is also prime. They are not well-known, even though Belphegor's Prime $1000000000000066600000000000001$ has some fame. A fun fact: palyndromic primes whose center is $666$ are called beastly palindromic primes. Perhaps a fitting name.

Safe primes are those primes $p$ of form $p=2q+1$, where $q$ is another prime. They are of strong cryptographic interest.

Sophie-Germain primes are the converse of safe primes, they are primes $p$ such that $q=2p+1$ is another prime. Of course, they share the relevance of safe primes.

All comparisons drawn, we get the following result.

Star class	Frequency	Prime number class	Frequency
O	0.00003%	Even primes	0.000025%
B	0.12%	Mersenne primes	0.12%
A	0.61%	Circular primes	0.79%
F	3.00%	Palindromic primes	1.67%
G	7.60%	Safe primes	7.76%
K	12.00%	Sophie-Germaine primes	13.44%
M	76.00%	all other primes	76.21...%

Plotting the galaxy

We now have everything we need: our seven prime number classes, their respective colors, and the interval $[0,40000]$. All that remains is to plot them. This just takes a few lines in Python, resulting in the picture below.

Keen observers might notice some packs of purple mist in the background. I added as nebulae Carmichael's numbers - which are not prime! The surprising fact about them is that they manage to fool all possible instances of Fermat's primality test in thinking they are prime, while they are not. Being somewhat rare and deceiving a famous primality test, it only seemed fitting to grant them a spot.